La definición de probabilidad se produjo debido al deseo del ser humano por conocer con certeza los eventos que sucederán en el futuro, por eso a través de la historia se han desarrollado diferentes enfoques para tener un concepto de la probabilidad y determinar sus valores.
EVENTOS O SUCESOS:
EVENTO SIMPLE: Definen una sola característica del evento. Ocurren cuando solamente miro un espacio muestral.
EVENTO COMPUESTO: Es un conjunto de eventos simples. Estoy componiendo espacios muestrales.
Partición de un espacio muestral
Son todas aquellas divisiones mutuamente excluyentes y colectivamente exhaustivas que se pueden realizar sobre un espacio muestral. Es por este motivo que puedo tener como máximo tantas particiones como eventos tenga el espacio muestral.
Dos eventos son mutuamente excluyentes cuando esos eventos son particiones de un mismo espacio muestral. En otras palabras, dos eventos A y B son mutuamente excluyentes si la ocurrencia de uno implica la no ocurrencia del otro.
Dos eventos son colectivamente exhaustivos cuando en conjunto involucran a la totalidad del espacio muestral. Es decir, la unión de los conjuntos que los representan conforman el espacio muestral.
La unión de dos conjuntos (AUB) está dada por el conjunto de todos los resultados que pertenecen al evento A, todo lo que pertenece a B, y todo lo que pertenece a A y B
Cuando me interesa definir una unión inclusiva no me interesan los valores repetidos, entonces los saco del conjunto A o del conjunto B
En este caso solo nos van a interesar los elementos que pertenecen a A o que pertenecen a B. Aquellos que pertenezcan a A y a B a la vez no los vamos a contabilizar.
La intersección de dos conjuntos (AՈB) está dada por el conjunto de los resultados que pertenecen tanto a A como a B simultáneamente. Es simplemente la probabilidad de que ambos sucedan al mismo tiempo.
Conclusiones
ΩA = { A1 , A2 , A3 , …. , AK }
1) La cantidad máxima de particiones es igual al valor K. Podría hacer menos particiones pero no más.
2) ⋁𝑖,𝑗 ∴𝑃 (𝐴𝑖∩𝐴𝑗)=0. Significa: Para todo par de A sub algo, por ejemplo A1 con A5, A4 con A6, es decir, para toda comparación de a pares, la probabilidad conjunta entre cualquier partición A subalgo con cualquier A subalgo es Nula. No puede haber ningún elemento que pueda pertenecer a dos particiones a la vez. Sino no serían particiones.
3) ⋂𝐴𝑖𝐾𝑖=1= ⊘ ⇒ 𝐴1∩𝐴2∩𝐴3 ∩...∩𝐴𝑘= ⊘ ⟹𝑃(⋂𝐴𝑖)=0
4) ⋃𝐴𝑖= Ω𝐴𝐾𝑖=1 ⟹𝑃(⋃𝐴𝑖𝐾𝑖=1)=1 Me está diciendo que cuando uno todas las particiones obtengo como resultado el espacio muestral. Entonces la probabilidad de la unión de todas las particiones va a ser igual a 1.
Andréi Kolmogórov: Nacio el 25 de abril de 1903 en Tambov y murio el 20 de octubre de 1987 en Moscú. Fue un matemático ruso que realizó aportes de primera línea en los contenidos de teoría de la probabilidad y de topología. Estructuró el sistema axiomático de la teoría de la probabilidad, utilizando el lenguaje teoría de conjuntos, donde los elementos son eventos. Trabajó en lógica constructivista; en las series de Fourier; en turbulencias y mecánica clásica. Fundó la teoría de la complejidad algorítmica. En 1929, bajo la supervisión del matemático Nikolái Luzin, alcanzó el doctorado en la Universidad Estatal de Moscú.
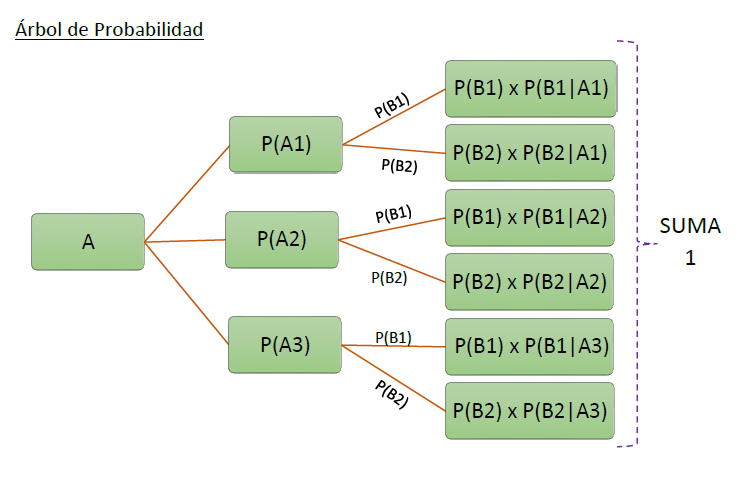
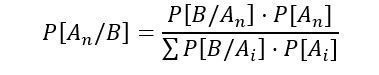Andrei Kolmogorov definió la medida o función de probabilidad mediante una serie de axiomas.
Dado un espacio muestral Ω, llamamos Medida de probabilidad a una función P que tiene como conjunto de salida al espacio muestral (el dominio) y que tiene como conjunto de llegada a los números reales, siendo su imagen los números reales que pertenecen al intervalo [0,1] si satisface los siguientes axiomas:
A) Si A es un evento cualquiera, entonces P(A) ≥ 0
B) P(Ω) = 1
C) Si A1 ( i = 1,2…) son eventos mutuamente excluyentes entonces: P(A1 U A2 U …) = P(A1) + P(A2) + …
A partir de esos axiomas se puede llegar a las siguientes conclusiones:
• Conocida la probabilidad de un evento A, se puede conocer su complemento A mediante la siguiente relación: 𝑃(A^C)=1−𝑃(𝐴)
• La función de probabilidad está incluida en el intervalo real [0;1], es decir: 0≪𝑃(𝐴)≪1
• La probabilidad del evento vacío es nula, es decir 𝑃(⊘)=0
• Si A y B son dos eventos cualesquiera, entonces la probabilidad de su unión es: 𝑃(𝐴⋃𝐵)=𝑃(𝐴)+𝑃(𝐵)−𝑃(𝐴⋂𝐵)
• Si A, B y C son 3 eventos cualesquiera, entonces la probabilidad de su unión es: 𝑃(𝐴∪𝐵∪𝐶)=𝑃(𝐴)+𝑃(𝐵)+𝑃(𝐶)−𝑃(𝐴∩𝐵)−𝑃(𝐵∩𝐶)+𝑃(𝐴∩𝐵∩𝐶)
• Si A está incluida en B, entonces la probabilidad de A es menor o igual a la probabilidad de B. 𝐴⊑𝐵⟹𝑃(𝐴)≤𝑃(𝐵)
• Si A esta incluido en B, entonces la probabilidad de la intersección de los dos conjuntos coincide con la probabilidad de A: 𝐴⊑𝐵⟹𝑃(𝐴∩𝐵)=𝑃(𝐴)
Voy a evaluar cuál es la probabilidad de que ocurra B habiendo ocurrido A: P(B l A)
Y la probabilidad de que ocurra A habiendo ocurrido B: P(A l B)
Entonces: 𝑃(𝐴|𝐵)= 𝑃(𝐴𝑦𝐵)𝑃(𝐵) ⟹𝑃(𝐴𝑦𝐵)=𝑃(𝐵)×𝑃(𝐴|𝐵)
𝑃(𝐴|𝐵)= 𝑃(𝐴𝑦𝐵)𝑃(𝐵): Formalización Matemática
𝑃(𝐴𝑦𝐵)=𝑃(𝐵)×𝑃(𝐴|𝐵): Formula
𝑃(𝐵|𝐴)= 𝑃(𝐵𝑦𝐴)𝑃(𝐴) ⟹𝑃(𝐵𝑦𝐴)=𝑃(𝐴)×𝑃(𝐵|𝐴)
Dos eventos A y B son estadísticamente independientes si la ocurrencia de uno no afecta la probabilidad de ocurrencia del otro, es decir que:
P(A|B) = P(A)
Ejemplo:
A: Cara superior de un dado lanzado con cubilete.
B: Calificación obtenida en la materia.
P(B=7|A=1) = P(B=7)
EVENTOS INDEPENDIENTES ≠ EVENTOS MUTUAMENTE EXCLUYENTES
Si A y B son dos eventos mutuamente excluyentes, entonces la unión de ambos eventos será igual a la suma de los eventos simples:
P(AUB) = P(A) + P(B) – P(AyB)
P(AyB): Para Eventos mutuamente excluyentes la probabilidad de que ocurra A y B va a ser igual a cero, ya que no pueden suceder a la vez.
Entonces…
P(AUB) = P(A) + P(B)
La probabilidad marginal de ocurrencia de un evento es igual a la suma del producto (multiplicación) de las probabilidades marginales de los eventos condicionantes por las probabilidades condicionales de ocurrencia del evento a estudiar dadas las ocurrencias de sus respectivas particiones. En otras palabras, la probabilidad marginal de que ocurra B es igual a la suma de las probabilidades conjuntas entre B y cada una de las particiones del evento.
Para saber como es la formalización haz click aquí.
Thomas Bayes: Nacio en Londres, Inglaterra en 1702 y murio en 1761 , Royal Tunbridge Wells. Fue un matemático británico y ministro presbiteriano. Su obra más conocida es el Teorema de Bayes. Estudió el problema de la determinación de la probabilidad de las causas a través de los efectos observados. El teorema que lleva su nombre se refiere a la probabilidad de un suceso condicionado por la ocurrencia de otro suceso. Más específicamente, con su teorema se resuelve el problema conocido como de la probabilidad inversa. Bayes fue uno de los primeros en utilizar la probabilidad inductivamente y establecer una base matemática para la inferencia probabilística.
Actualmente, con base en su obra, se ha desarrollado una poderosa teoría que ha conseguido notables aplicaciones en las más diversas áreas del conocimiento.
La visualización del teorema de Bayes por la superposición de dos árboles de decisión
Formalización
Fórmula del teorema de Bayes:
B es el suceso sobre el que tenemos información previa y A(n) son los distintos sucesos condicionados. En la parte del numerador tenemos la probabilidad condicionada, y en la parte de abajo la probabilidad total.
FCE-UBA
Av. Córdoba 2122.
Ciudad Autónoma de Buenos Aires. Argentina.
Diego Parrás
Aldana Tedesco